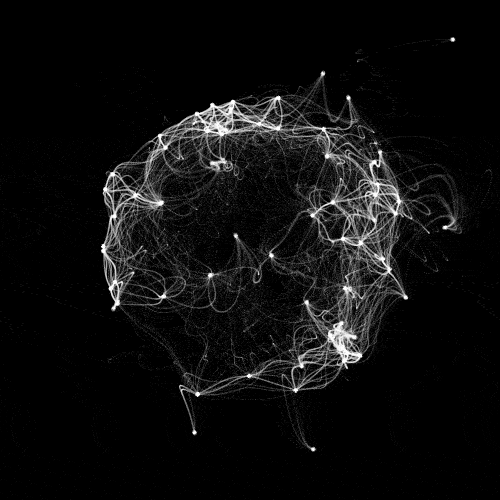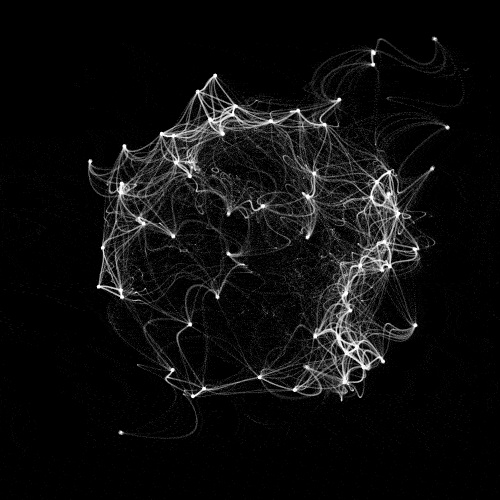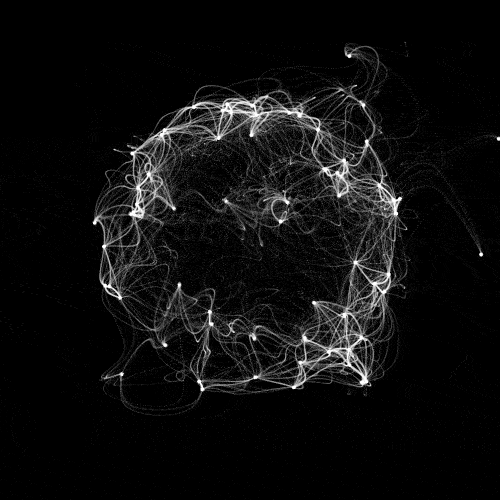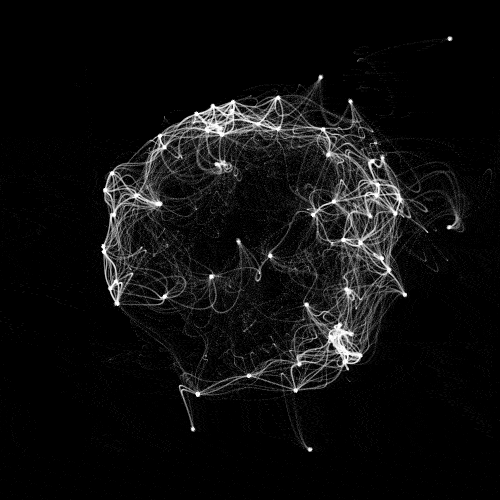
Sun connections
code
comments
First there is a set of points, with different random parameters. Each point moves around a random position (x0,y0), with a looping noise-based path. How to make a noise loop is explained in this post, there's also a video about it by the coding train on youtube. OpenSimplexNoise is used instead of Processing noise function, but it's similar.
So the formulas to get the points' position loops are basically like this:
- x = x0 + L*noise(seed + r*cos(t), r*sin(t))
- y = y0 + L*noise(2*seed + r*cos(t), r*sin(t))
The random (x0,y0) position is set using formulas so that it's distributed to have this sphere like shape, though this is done in 2D. L is a parameter for how large the movement is, and r how much we have varation with noise.
Now comes the tricky part: for each pair {i,j} of points, how to draw these connections between them. Let's say we have a parameter q in [0,1] where at 0 we're on dot i, at 1 we're on dot j, and in between we'll be on the curve. At q, the dot j is seen with the delay delayFactor*(1-q) where delayFactor is a parameter we can tune. No delay when we're at q=1, on j, and delayFactor when we're on i. Still at q, the dot i is seen with the delay delayFactor*q. No delay when we're at q=0 on i and delayFactor when we're on j. So we have two seen dot positions a and b, seen with these delays when we're at q. To get our current position on the curve we do this linear interpolation: lerp(a,b,q).
more information and links
Year: 2018
On bleuje site: https://bleuje.com/gifanimationsite/single/sunconnections/
On social media:
- tumblr: https://necessary-disorder.tumblr.com/post/170688287343/approximated-sun
- twitter: (TODO: find link)